Running Deep Neural Networks on Bitcoin
We have implemented a deep neural network for the classification of handwritten digits. The already trained model runs fully on-chain. It is trained offline using the MNIST dataset of handwritten digits. The model takes an image of 28x28 grayscale pixels and outputs a digit from 0 to 9.

Introduction to Deep Neural Networks
An artificial neural network is a construction inspired by biological neural networks. The network learns by being exposed to a large number of labeled examples of data. This process is also referred to as supervised learning.
The network is made up of several components: neurons/nodes, connections, biases, and activation functions. These components are grouped together consecutively into layers. The first layer is called the “input layer”, where data gets passed into the network, and the last one the “output layer”, by which the network returns its output. A very simple neural network contains only these two layers. To improve the performance we can add one or more “hidden layers” between the two. Networks with hidden layers are called “deep neural networks” (DNN).
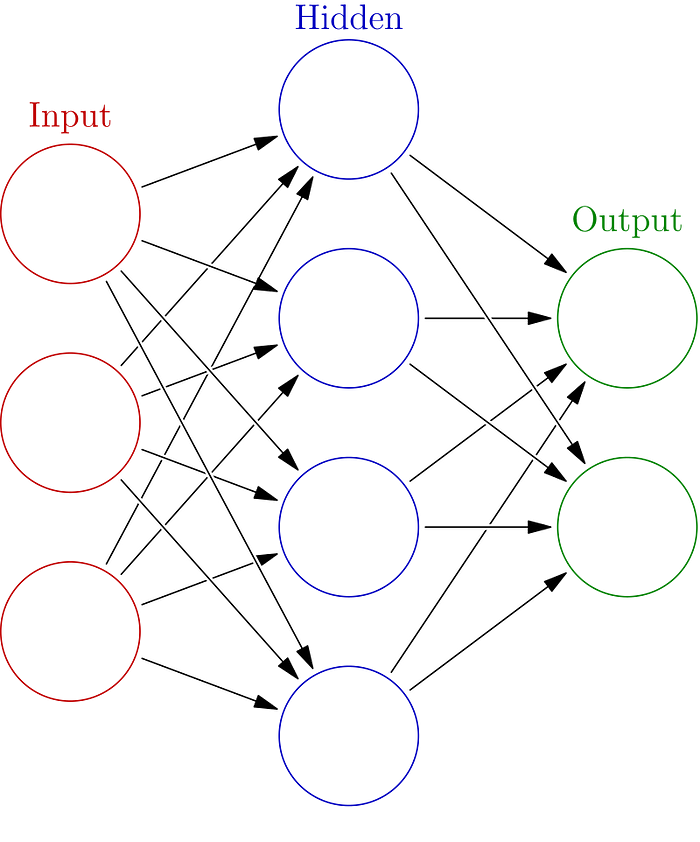
Each connection between neurons in the network is weighted with a specific value. Each neural also has a value called a “bias” which gets added to the sum of its inputs. Learning is the process of finding a set of these weights and biases, so that the network will return a meaningful output given some input.
To get a good intuitive sense of how deep neural networks work under the hood, we recommend watching a short video series on the topic.
The Network Architecture
The DNN for MNIST handwritten digits is made up of an input layer of 784 (28 x 28) nodes, a hidden layer of 64 nodes and an output layer of 10 nodes (number of possible classes/digits). The layers are all fully-connected, which makes the network contain a total of 501760 (784 * 64 * 10) connections.
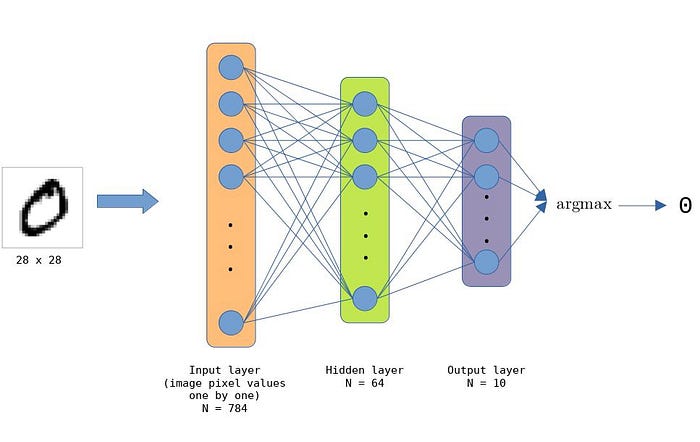
Nodes in the hidden layer use the ReLU activation function. Argmax is used on the output nodes to get the right value, i.e., digit of the classification.
Train the Model
The DNN is trained using Keras. With our outlined architecture of the network and by using the RMSprop optimizer for training, the model is able to achieve 98 % classification accuracy after 50 epochs.
Once the model is trained the weights and biases must be exported in a format that we can use in an sCrypt smart contract. For performance reasons, we encode these values in bytes, not arrays.
Implementation
We have implemented the DNN above, similar to the single layer neural network (a.k.a., a perceptron) we have implemented before. The full code can be found on GitHub.
The function predict() takes in the initial values of the input layer. In our case that is the serialized values of a handwritten image. It returns an integer which represents the classification result, i.e. the number on the image.
Because sCrypt does not support native floating point numbers, we use fixed-point representations by simply scaling values by 10⁸. For example, 0.86758491 becomes an integer 86758491. When multiplying two values we rescale the result, i.e. divide it by 10⁸.
Potential Use Cases
DNNs like this could be used in many ways inside a smart contract. For example, you can train a model to recognize if an image contains a hotdog with a certain accuracy. Users are incentivised to scrape the Internet for such photos and automatically get paid in bitcoin micropayments for submitting them. These photos can be collected to train the model and improve its accuracy.
